isi group

Density functional study of endohedral germanium clusters

Our interest in the chemistry of main group elements clusters is part of an ongoing collaboration with Prof. R. Bruce King, which resulted in two PhD theses, supervised by Prof. Ioan Silaghi-Dumitrescu and Prof. Bruce King. Part of the results of this research, obtained by Dr. Alexandru Lupan, is presented below; the work in the vast field of germanium clusters is currently continued by Dr. Matei M. Uţă.

Effect of the electron count on the geometry of eight-atom germanium clusters

Development of main group cluster chemistry has two historical landmarks: the discovery of the neutral boron hydrides by Alfred Stock and the discovery of anionic clusters of post-transition metals (the so-called Zintl phases) by Eduard Zintl. Wade noticed that the stability of the deltahedral boranes and isoelectronic carboranes was related to the presence of 2n+2 skeletal electrons(Wade, K., Chem Comm., 1971, 792; Wade, K., Adv. Inorg. Chem. Radiochem., 1976, 18, 1). This idea was then used by Mingos to develop the polyhedral skeletal electron pair approach (Mingos, D.M.P., Nature Phys. Sci., 1972, 99, 236; Mingos, D.M.P., Accts. Chem. Res., 1984, 17, 311) for understanding the structural diversity of the polyhedral boranes. That is why these theoretical electron-counting models are called "Wade-Mingos rules", applicable not only to boranes but also to main group and transition metal clusters such as the polyhedral metal carbonyl clusters.

The Ge₈^2- cluster has the 18 skeletal electrons (= 2n + 2 for n = 8) required by Wade-Mingos rules for a closo deltahedron and is thus isoelectronic with the known deltahedral borane anion B₈H₈^2- and the isoelectronic neutral dicarbahexaborane Me₂C₂B₆H₆, which have (if idealized to equal atoms and therefore symmetry-equivalent interactions) D_2d bisdisphenoidal structures. However, the lowest energy structure 1-1 for Ge₈^2- is not the bisdisphenoid but the Td tetracapped tetrahedron already suggested for E₈^2- (E = Si, Ge, Sn) as spherical (homo)aromatic systems.

Figure 1. Some of the optimized structures found for Ge₈^2-

The optimized structures for Ge₈^2- are presented in figure 1. The molecular orbital (MO) pattern for 1-1 exhibits a spherical harmonic pattern with a lowest lying fully symmetric S+ orbital followed in sequence by three degenerate P orbitals, three degenerate D orbitals (xy, xz, yz), the antisymmetric S- orbital, the remaining two D orbitals (z², x²-y²), and the seven cubic F orbitals with a degeneracy sequence 1, 3, 3, with the last triply degenerate set as the HOMO. The LUMO is then a triply degenerate set of the first G orbitals with a hexagonal prismatic lobal pattern. Thus the HOMO-LUMO energy gap in Td Ge₈^2- (1-1) corresponds to the end of the F skeletal orbitals and the beginning of the G skeletal orbitals as expected for a spherical aromatic system.

The D_2d bisdisphenoidal structure 1-2 for Ge₈^2-, required by the Wade-Mingos rules and known experimentally in B₈H₈^2-, was found at 3.9 kcal/mol higher energy than the T_d structure 1-1. The 8-vertex bisdisphenoid has four pairwise degenerate edges, which are those of type 55(44) located in the subtetrahedron consisting of degree 5 vertices of the structure (black edges in figure 4.b), so that two successive processes involving opposite edges of this type (a pair related by a C₂-symmetry operation) converts one bisdisphenoid into another through a square antiprismatic intermediate. A bisdisphenoid is thus inherently fluxional. The other following optimized structures that were found for Ge₈^2- are ordered as follows:

• structure 1-3 at +10.1 kcal/mol (C_2v symmetry): a trigonal prism with caps on two of the rectangular faces obtained by a square-diamond process on a square antiprism.
• structure 1-4 at +12.4 kcal/mol (C_s symmetry): an octahedron with caps on a pair of faces sharing a vertex.
• structure 1-5 at +13.8 kcal/mol (C_s symmetry): a capped pentagonal bipyramid.
• structure 1-6 at +15.0 kcal/mol (D_3d symmetry): an octahedron with caps on two opposite faces.

The only one of these higher energy structures that has been realized experimentally in isolable eight-vertex clusters having 18 skeletal electrons is the square antiprism related to 1-3 but without the distortion from D_4d to C_2v symmetry through a square-diamond process. Such a square antiprism is found in the anion (C₁₃H₉)₈Ga₈^2- (C₁₃H₉ = fluorenyl), which is clearly isoelectronic and isolobal with Ge₈^2-. In addition, a square antiprismatic metal carbonyl anion also with 18 skeletal electrons and thus isoelectronic with Ge₈^2- is the cobalt carbonyl derivative Co₈C(CO)₁₈^2-, in which four of the 18 skeletal electrons come from the valence electrons of the interstitial carbon atom in the center of the Co₈ square antiprism.

I.1. Electron-rich Ge₈^4- structures

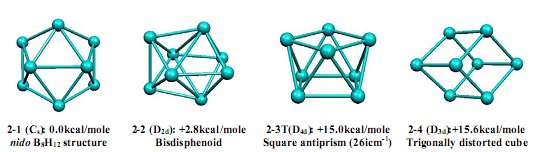
An anion of stoichiometry Ge₈^4- has the 20 skeletal electrons required by the Wade-Mingos rules for a nido structure with a single non-triangular face (20 = 2n + 4 for n = 8). In fact the lowest energy structure found for Ge₈^4- (2-1 in figure 2) is a C_s nido structure with a hexagonal open face closely related to that found by X-ray diffraction for B₈H₁₂ originating from an icosahedral fragment, related to that of EtNH₂B₈H₁₂NHEt) and the isoelectronic tetracarbaoctaborane Et₄B₄C₄H₄. The next structure (2-2) for Ge₈^4- of only slightly higher energy than 2-1 (+2.8 kcal/mol) is a D_2d bisdisphenoid similar to that found by X-ray diffraction for the metallaborane (η⁵-C₅H₅)₄Ni₄B₄H₄ with 20 skeletal electrons, namely 3 from each η⁵-C₅H₅Ni vertex and 2 from each BH vertex. Two higher energy structures were found for Ge₈^4- at ~15 kcal/mol above the global minimum 2-1 (figure 2). The first such structure is a triplet D_4d square antiprism 2-3T at +15.0 kcal/mol. The triplet nature of this structure is consistent with a half-filled doubly degenerate highest occupied MO. The other structure 2-4 at a similar energy (+15.6 kcal/mol) is a D_3d trigonally distorted cube.

Figure 2. The four lowest energy optimized structures for Ge₈^4-

I.2. Hyperelectronic Ge₈^6- clusters

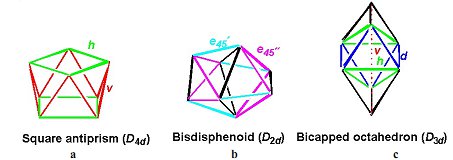
The stoichiometry Ge₈^6- has the 22 skeletal electron configuration suggested by the Wade-Mingos rules for an arachno structure with two open (i.e., non-triangular) faces or one large open face. The most symmetrical arachno eight-vertex structure is the D_4d square antiprism, which is found for Ge₈^6- as the global minimum 3-1 (figure 3). This structure is found experimentally in the dications E₈²⁺ ( E = Bi and Sb) isoelectronic and isolobal with Ge₈^6-. In square antiprismatic Ge₈^6- the ratio of the intersquare distance (v in figure 4.a) to the intrasquare distance ( h in figure 4.a) is computed to be 0.98 as compared with experimental v/h values of 0.97 for Sb₈²⁺ in Sb₈[GaCl₄]₂ and 1.00 for Bi₈²⁺ in Bi₈[AlCl₄]₂ indicating close agreement between the calculated value for Ge₈^6- and the experimental values for E₈²⁺ ( E = Bi, and Sb). Energetically close to the square antiprism for Ge₈^6- by less then 1.0 kcal/mol is the deformed cube 3-2, which is related to the square antiprism 3-1 by a rotation of one of the square faces by 45° with a concurrent quadruple diamond-square-diamond process.

Figure 3. The four optimized structures for Ge₈^6-

Two other computed structures for Ge₈^6- were found within 25 kcal/mol of the global minimum 3-1 (figure 3). The triplet structure 3-3T at +9.5 kcal/mol above 3-1 is derived from a bisdisphenoid by lengthening four equivalent edges to 3.55 Å while preserving the D_2d symmetry. Another triplet structure 3-4T at +22.5 kcal/mol above 3-1 appears to be related to structure 3-4 for Ge₈^4- by half-filling a doubly degenerate LUMO of 3-4, thereby leading to triplet spin multiplicity.

Figure 4. (a) The two different types of edges (h,ν) in the D_4d square antiprism; (b) The edges e45´ (cyan) and e45˝ (magenta) in the D_2d bisdisphenoid; (c) The distances v (red), h (green), and d (blue) in the D_3d bicapped octahedron.

I.3. The 16 skeletal electron cluster Ge₈

A neutral Ge8 cluster is certainly unstable with respect to polymerization to bulk germanium metal. However, computations on neutral Ge₈ are of interest in order to characterize the relative stabilities of various eight-vertex polyhedra in 16 skeletal electron systems. Examples of such eight-vertex 16 skeletal-electron clusters are the isoelectronic D_2d bisdisphenoidal species (η⁵-C₅H₅)₄Co₄B₄H₄ and (η⁵–C₅H₅)₄Fe₄C₄H₄ as well as octachlorooctaborane, B₈Cl₈. The skeletal bonding in these derivatives has been interpreted as consisting of 3c-2e bonds in eight of the 12 faces of the bisdisphenoid as it has 16 = 2n skeletal electrons for n = 8.

The three lowest lying computed structures for Ge₈, namely 4-1, 4-2 and 4-3 at 0.0, +4.3 and +5.3 kcal/mol (figure 5), respectively, all exhibit only low symmetry (C_s or C₂). Their geometries are related to a capped pentagonal bipyramid or a bicapped six-vertex nido polyhedron with one quadrilateral face. The Wade-Mingos rules for a neutral Ge₈ structure suggest a capped pentagonal bipyramid and thus symmetry no higher than C_s or a bicapped nido 6-vertex structure with symmetry no higher than C₂. For this reason, low symmetry structures for Ge₈ with energies at or near the global minimum are not at all surprising. The occurrence of the edge-bridged pentagonal bipyramid structure 4-1 and the capped pentagonal bipyramid structure 4-4 within 5.3 kcal/mol of each other suggests that capping a pentagonal bipyramid leads to a highly fluxional structure, possibly related to its relatively low symmetry.

Figure 5. The three lowest energy optimized structures for Ge₈.

The bisdisphenoid structure found experimentally for the 16 skeletal electron species (η⁵-C₅H₅)₄Co<B₄H₄ and (η⁵-C₅H₅)₄Fe₄C₄H₄ was not found as a minimum within 30 kcal/mol of the global minimum 4-1. Attempts to optimize Ge₈ starting with the D_2d bisdisphenoid structure preserving D_2d symmetry led to a structure with a significant imaginary vibrational frequency (80i) indicating that it is a saddle point rather than a global minimum.

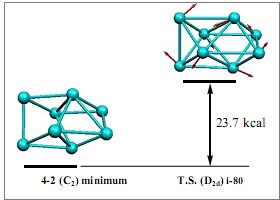
Figure 6. The relationship between the minimum 4-2 and the corresponding bisdisphenoid geometry representing the transition state

The bicapped nido 6-vertex polyhedron 4-2 was obtained from the bisdisphenoidal structure by distortions along the modes of the largest imaginary frequencies. Thus in the absence of η⁵-C₅H₅M (M = Co, Fe) groups at the degree 5 vertices of the bisdisphenoid, two of the edges of the bisdisphenoid, rupture in a double diamond-square process to give a polyhedron with two quadrilateral faces (4–2). The transition metal vertices in the known eight-vertex complexes (η⁵-C₅H₅)₄Co₄B₄H₄ and (η⁵-C₅H₅)₄Fe₄C₄H₄ appear necessary to preserve all four degree 5 vertices of the bisdisphenoid.

I.4. Cationic Ge₈^z Clusters

In the case of the eight-vertex clusters with 14 or fewer skeletal electrons isoelectronic and isolobal with cationic Ge₈^z+ clusters the only experimentally-known analogue structure is the Tl₈^6- cluster in Cs₈Tl₈O, which is the first example of a hypoelectronic bare post-transition element eight vertex cluster. Possible structures for such clusters were studied in order to suggest possible future synthetic targets either in germanium chemistry or in the chemistry of the group 13 elements (e.g., Ga, In, Tl) where bare hypoelectronic clusters are more likely.

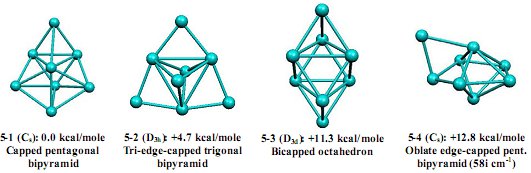
The global minimum 5-1 for the dication Ge₈²⁺ is a low symmetry C_s capped pentagonal bipyramid (figure 7). The next structure 5-2 at +4.7 kcal/mol above the global minimum 5-1 in the Ge₈²⁺ system can be described as a trigonal bipyramid with bridges along each of the three equatorial-equatorial bridges thereby retaining the D_3h symmetry of the original trigonal bipyramid. The Wade-Mingos rules suggest a bicapped octahedron for Ge₈²⁺ with 14 skeletal electrons. The next structure in terms of energy, namely 5-3 at +11.3 kcal/mol above the global minimum 5-1, is an octahedron with a pair of opposite faces capped, thereby retaining D_3d symmetry. This structure was found experimentally for Tl₈^6- (isoelectronic to Ge₈²⁺) in Cs₈Tl₈O cluster. The d/h ratio of 0.95 for the experimentally-obtained Tl₈^6- is very close with the d/h ratio of 0.93 for Ge₈²⁺ (5-3) which is an excellent agreement, considering the different elements and the different charge.

Figure 7. The four lowest optimized structures for Ge₈²⁺

The next higher energy structure for Ge₈²⁺ at +12.8 kcal/mol (5-4) is an edge-bridged pentagonal bipyramid. This structure is closely related to structure 4-1 but compressed so that the axial-axial distance in the underlying pentagonal bipyramid is only 2.88 Å, similar to the length of an edge. This type of compression upon reduction of the skeletal electron count by two electrons was previously noted both computationally and experimentally in the six vertex group 13 clusters E₆^z- (E = In, Tl) where the clusters E₆^8- are regular octahedra and the clusters E₆^6– are compressed octahedra. The hypoelectronic cluster undergoes a Jahn-Teller distortion with a pronounced axial compression, a pathway that serves to the stabilization and reduction of the cluster charge. This idea is supported also by extended Hückel calculations in which a regular octahedron is distorted to D_4h symmetry structure.

Relevant publications:

Density Functional Theory Study of 11-Atom Germanium Clusters: Effect of Electron Count on Cluster Geometry, R.B. King, I. Silaghi-Dumitrescu, A. Lupan, Inorg. Chem., 2005, 44(10), 3579-3588.

Density Functional Theory Study of Eight-Atom Germanium Clusters: Effect of Electron Count on Cluster Geometry, R.B. King, I. Silaghi-Dumitrescu, A. Lupan, Dalton Trans., 2005, 10, 1858-1864.

Density Functional Theory Study of 8- and 11-vertex Polyhedral Borane Structures: Comparison with Bare Germanium Clusters, R.B. King, I. Silaghi-Dumitrescu, A. Lupan, Inorg. Chem., 2005, 44(22), 7819-7824.

Germanium cluster polyhedra: a density functional theory study, I. Silaghi-Dumitrescu, A. Kun, A. Lupan, R.B. King, Lect. Series on Computer and Comput. Sci., 2005, 4A, 804-806.

New low symmetry low energy structures of 11-atom bare germanium clusters: A density functional theory study, R.B. King, I. Silaghi-Dumitrescu, A. Lupan, Phys. Chem., 2006, 327(2), 344-350.

The Shapes of Hypoelectronic Six-Vertex Anionic Borane Clusters: Effects of the Countercations, R.B. King, I. Silaghi-Dumitrescu, A. Lupan, A. Kun, Main Group Chem., 2006, 4(4), 291-302.

Density Functional Theory Study of 10-Atom Germanium Clusters: Effect of Electron Count on Cluster Geometry, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, Inorg.Chem., 2006, 45, 4974-4981.

Density Functional Theory Study of Twelve-Atom Germanium Clusters: Conflict Between the Wade-Mingos Rules and Optimum Vertex Degrees, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, J.Chem.Soc. Dalton Trans., 2007, 364-372.

Beyond the Wade-Mingos Rules in Bare 10- and 12-Vertex Germanium Clusters: Transition States for Symmetry Breaking Processes, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, J.Chem.TheoryComput., 2008, 4, 209-215.

Beyond the Icosahedron: A Density Functional Theory Study of 14-Atom Germanium Clusters, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, Eur.J.Inorg.Chem., 2008, 25, 3996-4003.

Polyhedral Structures with Three-, Four-, and Five Fold Symmetry in Metal-Centered Ten-Vertex Germanium Clusters, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, Chem.Eur.J., 2008, 14, 4542-4550.

The Unique Palladium-Centered Pentagonal Antiprismatic Cationic Bismuth Cluster: A Comparison of Related Metal-Centered 10-Vertex Pnictogen Cluster Structures by Density Functional Theory, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, Inorg.Chem., 2009, 48 (17), 8508-8514.

Endohedral Nickel, Palladium, and Platinum Atoms in 10-Vertex Germanium Clusters: Competition between Bicapped Square Antiprismatic and Pentagonal Prismatic Structures, R.B.King, I.Silaghi-Dumitrescu, M.M.Uţă, J.Phys.Chem.A, 2009, 113 (3), 527-533.