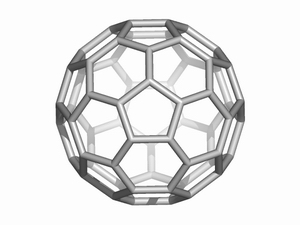
[60] Fullerena


Graph theory applied in the study of molecular structures represents an interdisciplinary science, called chemical graph theory or molecular topology. By using tools taken from the graph theory, set theory and statistics it attempts to identify structural features involved in structure-property activity relationships. The partitioning of a molecular property and recombining its fragmental values by additive models is one of its main tasks. Topological characterization of chemical structures allows the classification of molecules and modeling unknown structures with desired properties. In the following some details are given.
A molecular graph can be represented by: a sequence of numbers, a polynomial, a single number or a matrix. These representations are aimed to be unique, for a given structure. Topological matrices can be accepted as a rational basis for designing topological indices.
The main types of matrix descriptors studied by TOPO GROUP CLUJ are:
A single number, representing a chemical structure, in graph-theoretical terms, is called a topological descriptor. Being a structural invariant it does not depend on the labeling or the pictorial representation of a graph. Despite the considerable loss of information by the projection in a single number of a structure, such descriptors found broad applications in the estimation and prediction of several molecular properties and also in tests of similarity and isomorphism.
When a topological descriptor correlates with a molecular property, it can be denominated as molecular index or topological index (TI).
The main types of 2D and 3D molecular descriptors studied by TOPO GROUP CLUJ are:
The investigation of molecular structure involves research on its constitution (i.e. the number and chemical identity of atoms and bonds joining them) and configuration in 3D-space.
Molecules show various types of geometrical symmetry. The symmetry is reflected in several molecular properties, such as dipole moments, IR vibrations, 13C - NMR signals etc., properties which are dependent on the spatial structure of molecules. The molecular topology reveals a different type of symmetry: the TOPOLOGICAL SYMMETRY (i.e. constitutional symmetry). It is defined in terms of connectivity, as a constitutive principle of molecules and expresses the equivalence relationships between elements of graph: vertices, bonds or larger subgraphs. It makes use of groups theory formalism in modeling an N - dimensional space. The geometrical aspects are disregarded.
SIMILARITY (or relatedness) of molecular structures expresses the common features occurring within a set of molecules. It is established on the ground of various criteria and procedures. Both symmetry and similarity provide equivalence classes: the first one at the level of molecular graph and its subgraphs while the last one among the members of a whole set of molecules. The two notions are rather interrelated.
The main subjects studied by TOPO GROUP CLUJ are:
Property Modeling: QSPR (Quantitative Structure -Proprety Relationship) / QSAR (Quantitative Structure-Activity Relationship)
The central problem in QSPR (Quantitative Structure -Proprety Relationship) l QSAR (Quantitative Structure-Activity Relationship) is to convert chemical stmctures into molecular descriptors that are relevant to a certain physico-chemical property or biological activity.
Although various physico-chemical properties may be subjected to QSPRlQSAR studies, the major application field of these models is drug discovery. Classically, drug discovery mainly relied on chance and masive screening of Iarge libraries of synthesized or natural compounds. By contrast, computer-aided drug design, CADD, is an approach to rational drug design made possible by the recent advances in computational chemistry (in its various fields, such as molecular gaphics, quantum chemistry, molecular mechanics, molecular dynamics, library searching, prediction of physico-chemical and biological properties) and, of course, in computer science.
Many physico-chemical properties can be satisfactorily correlated with the topostructural and topochemical features. Topological indices are among the simplest and efficient descriptors for QSPR/QSAR. In principle, these are mathematical objects, wihtout a precise physical meaning. However, they may express the topological shape or may correlate with the molecular volume or surface area, as is shouwn in the pages of this book.
TOPO GROUP CLUJ performed various QSPR and QSAR studied by the aid of CLUJ Property Descriptors, calculated by TOPOCLUJ program, designed both as Graph Theoretical Module and Q-SEARCH package.
Fullerene chemistry is nowadays a well-established field of both theoretical and experimental investigations. The initial fascinating appeal, coming from their beautiful symmetry shifted later to real chemistry. Carbon allotropes with finite molecular cage structures have been functionalized or inserted in supra-molecular assemblies.

TOPO GROUP CLUJ has performed studies on operations on maps, useful in understanding the isomerisation reactions in fullerenes. Periodic fulleroids (see figure) is one of the original research fields
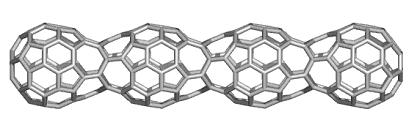
Cylindrical nanostructures with various covering are theoretically studied by TOPO GROUP CLUJ

A novel, original, procedure for generating "in silico" nanotubular structures was implemented in a TORUS Software package.
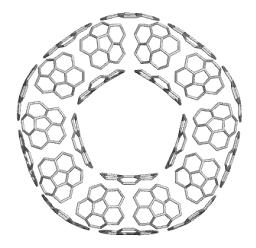
Since a spherical surface cannot be tiled by pure hexagonal pattern, the scientists looked for other surfaces capable to allow a full polyhex tessellation. Such surfaces are cylinders (e.g., open nanotubes) and tori, both of them identified in the products of laser irradiation of graphite. According to Euler's formula: v - e + f = 2 - 2g (v, e, f, g being respectively the number of vertices, number of edges, number of faces, and genus) a torus is of genus one while a sphere or a cylinder are of genus zero.
TOPO GROUP CLUJ performed a TORUS program for generating toroidal fullerenes (covered by various polygons).